Μάθημα : Μαθηματικά Προσανατολισμού Β' Λυκείου

Κωδικός : 5051030265

Μαθηματικά Προσανατολισμού Β' Λυκείου

5051030265  -  ΧΡΙΣΤΟΦΟΡΟΣ ΠΑΠΑΝΙΚΟΛΑΟΥ

Περιγραφή Μαθήματος

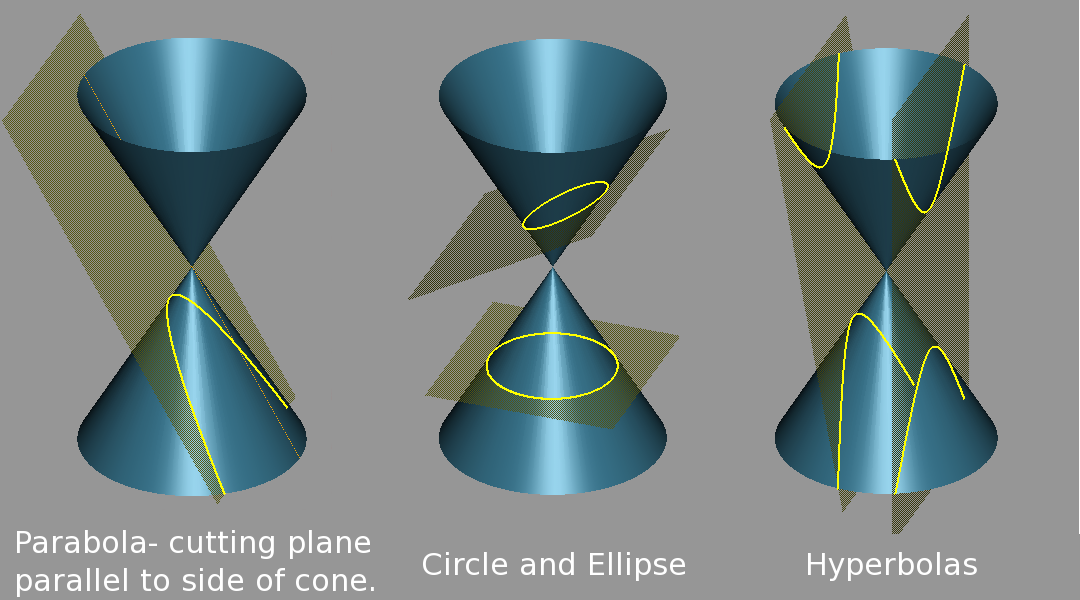
Μάθημα

Το μάθημα αυτό είναι μία πρώτη επαφή των μαθητών με τα διανύσματα και τις κωνικές τομές. Είναι βασικό ώστε να μάθουν τα παιδιά τρόπους απόδειξης μαθηματικών ισχυρισμών και να αποκτήσουν μία καλύτερη γεωμετρική εποπτεία του χώρου. 

Κεφάλαιο 1: Διανύσμστα

 

  • 22/09/25, σήμερα κάναμε μία εισαγωγή στα διανύσματα. Είδαμε τι είναι μέτρο, ομόρροπα, αντίρροπα και μάθαμε πώς αθροίζονται και αφαιρούνται δύο διανύσματα. 
  • 23/09/25, σήμερα κάναμε το διάνυσμα θέσης και λύσαμε ένα θέμα από την τράπεζα θεμάτων (το 21165) .
  • 30/09/25, σήμερα λύσαμε κάποιες ασκήσεις από το δωρεάν βιβλίο που θα ακολουθήσουμε στο μάθημα (σελίδες 7 έως 11) Μπορείτε να το κατεβάσετε εδώ.
    • Ασκήσεις για το σπίτι:  11 και 15 στις σελίδες 10 και 11 αντίστοιχα από το βιβλίο που κατεβάσατε
  • 03/10/25, σήμερα είδαμε ακόμα μερικές ασκήσεις πάνω στις πράξεις με διανύσματα. 
  • 08/10/25, σήμερα μπήκαμε στην παράγραφο 1.3 του σχολικού βιβλίου και λύσαμε την άσκηση 2 σελ 26 σχολικού το i ερώτημα (το ii για το σπίτι) και την άσκηση 3 σελίδας 17 από το βοήθημα που δεν προλάβαμε και την έχετε για το σπίτι.
  • 09/10/25, σήμερα κάναμε κάποιες ασκήσεις πάνω στις πράξεις με διανύσματα
  • 10/10/25, σήμερα κάναμε τη συνθήκη παραλληλίας διανυσμάτων και τη διανυσματική ακτίνα
  • 13/10/25, σήμερα κάναμε την άσκηση 4 σελίδας 27 του σχολικού βιβλίου 
  • 15/10/25, σήμερα είδαμε την άσκηση 5 και 7 σελίδας 27 του σχολικού και μπήκαμε στην επόμενη παράγραφο 1.4 Συντεταγμένες στο επίπεδο. Είδαμε τον άξονα και το μοναδιαίο διάνυσμα i
  • 16/10/25, σήμερα είδαμε το ορθοκανονικό σύστημα συντεταγμένων και τις συντεταγμένες διανύσματος. Μάθαμε πώς ένα διάνυσμα γράφεται σαν συνδυασμός των διανυσμάτων i και j.
  • 21/10/25, σήμερα μάθαμε να βρίσκουμε τις συντεταγμένες γραμμικού συνδυασμού διανυσμάτων, πότε ένα διάνυσμα είναι μηδενικό και πότε δύο διανύσματα είναι ίσα.  Οι ασκήσεις που λύνουμε μέσα στην τάξη είναι από το φύλλο εργσίας που σας έδωσα. 
  • 23/10/25, σήμερα είδαμε τις συντεταγμένες διανύσματος όταν γνωρίζουμε τα δύο άκρα του, τις συντεταγμένες μέσου ενός τμήματος και το μέτρο διανύσματος. 
  • 24/10/25, σήμερα είδαμε, τις ασκήσεις που σας είχα βάλει και μάθαμε επιπλέον τη συνθήκη παραλληλίας δύο διανυσμάτων και το συντελεστή διεύθυνσης. 
  • 30/10/25, σήμερα λύσατε εσείς ασκήσεις από την ενότητα 1.4 του βιβλίου.
  • 31/10/25, σήμερα λύσαμε τις υπόλοιπες ασκήσεις της Α ομάδας του βιβλίου από την παράγραφο 1.4
  • 05/11/25, μπήκαμε στην παράγραφο 1.5 εσωτερικό γινόμενο διανυσμάτων. Είδαμε τον ορισμό, λύσαμε μερικές εφαρμογές του ορισμού και είδαμε και την έκφραση του εσωτερικού γινομένου με τις συντεταγμένες καθώς και πότε δύο διανύσματα είναι κάθετα.
  • 12/11/25, σήμερα είδαμε ασκήσεις πάνω στο εσωτερικό γινόμενο
  • 13/11/25, είδαμε τις συνέπειες του ορισμού του εσωτερικού γινομένου και τις ιδιότητές του. 
  • 14/11/25, σήμερα είδαμε ασκήσεις από το βιβλίο. 
  • 20/11/25, πάλι είδαμε ασκήσεις από το βιβλίο
  • 27/11/25, είδαμε κάποιες ασκήσεις επαναληπτικές πάνω στα διανύσματα
Κεφάλαιο 2: Ευθεία
  • 04/12/25, σήμερα είδαμε πότε ένα σημείο ανήκει ή δεν ανήκει σε μία γραμμή. Αν δηλαδή επαληθεύει την εξίσωσή της ή όχι
  • 05/12/25, σήμερα είδαμε το συντελεστή διεύθυνσης της ευθείας και τη δεύτερη ώρα κάναμε τις συνθήκες παραλληλίας και καθετότητας δύο ευθειών.
  • 11/12/25, σήμερα είδαμε κάποιες ασκήσεις πάνω σε αυτά που κάναμε την προηγούμενη φορά. 
  • 12/12/25, σήμερα είδαμε κάποιες ασκήσεις πάνω στην ευθεία, πώς βρίοσκουμε δηλαδή την εξίσωσή της.
  • 20/12/25, είδαμε κάποιες ασκήσεις στην εύρεση εξίσωσης ευθείας και μπήκαμε και στην παράγραφο 2.2 μέχρι τη σελίδα 67.  
  • 08/01/26, είδαμε μία αντιπροσωπευτική άσκηση πάνω στην παράγραφο 2.2
  • 09/01/26, είδαμε ασκήσεις πάνω στην ευθεία και κάναμε μία επανάληψη για το διαγώνισμα στις 22/01
  • 15/01/26, σήμερα μπήκαμε στην παράγραφο 2.3 Εμβαδόν Τριγώνου και είπαμε τον τύπο απόστασης σημείου από ευθεία και τον τύπο του εμβαδού τριγώνου όταν ξέρουμε τα σημεία των κορυφών του. 
  • 16/01/26, σήμερα κάναμε μία τελευταία επανάληψη πριν το διαγώνισμα
Κεφάλαιο 3: Κύκλος
  • 23/01/26, σήμερα μπήκαμε στο κεφάλαιο Κύκλος, δείξαμε την εξίσωση του κύκλου με κέντρο το Ο(0,0), την εξίσωση του κύκλου με κέντρο το \(K(x_0, y_0)\) και την εφαπτομένη του κύκλου στο σημείο \(A(x_1,y_1)\). Επίσης λύσαμε τις ασκήσεις 1 και 5 της σελίδας 87 (δεν τις ολοκληρώσαμε αλλά θα τις συνεχίσουμε την επόμενη φορά)

Ημερολόγιο

Προθεσμία
Γεγονός μαθήματος
Γεγονός συστήματος
Προσωπικό γεγονός

Ανακοινώσεις

Όλες...